
Descrição
The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described. It is based on the Koch curve, which appeared in a 1904 paper entitled:"Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire", by the Swedish mathematician Helge von Koch.
The Koch Snowflake can be constructed by starting with an equilateral triangle, and then recursively altering each line segment s by dividing it in three segments of size s/3, forming a new triangle. Then, each segment can be divided infinitely.
The following figure shows the first four levels of the Snowflake.
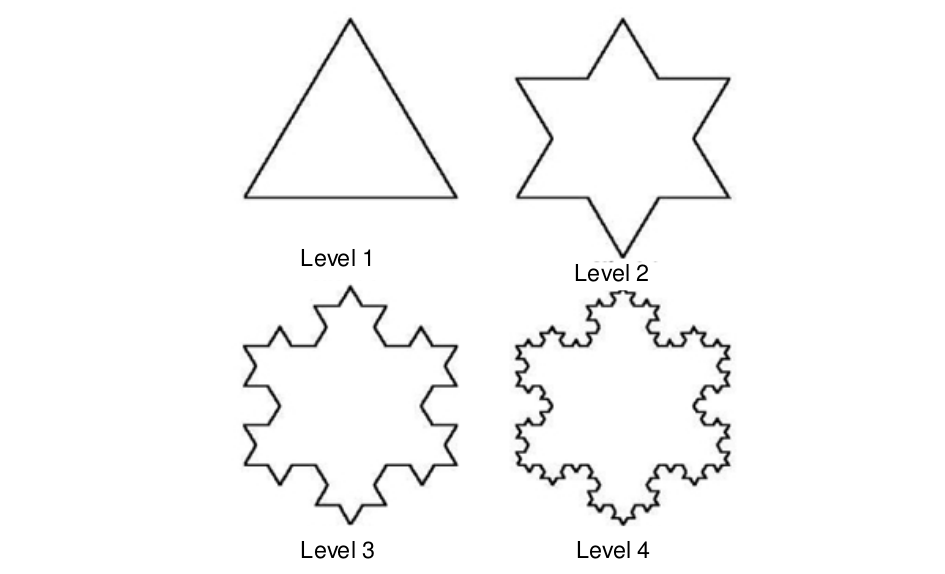
Helge von Koch, in his epoch, could not create a machine able calculate the total area of the Snowflake, but now you have all the necessary technology.
To calculate the area of the equilateral triangle, use the formula:
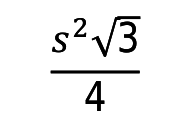
For all the calculations, consider using floating-point number with double precision
Entrada
The input consists of several test cases. Each line has a number S (0 < S < 100), a floating-point number with double precision that corresponds to the size of each segment of the triangle and the number of levels N (0 < N < 16) for which the Snowflake must evolve.
The final input case is defined by S and N equal to zero (0 0).
Saída
Print a line for each input with the total area of the Snowflake obtained considering the precision of 8 numbers after the decimal point.
| Exemplos de Entrada | Exemplos de Saída |
|---|---|
|
1 3 |
0.64150030
|
Efetue Login ou Cadastre-se para submeter uma solução.
Criado por Eduardo Sakaue (Fatec São José dos Campos) | Adaptado por erich.rodriguesf | Competição: Interfatecs 2014 2ª fase