Considere uma situação em que temos um conjunto de intervalos e precisamos implementar as seguintes operações de forma eficiente.
1) Adicionar um intervalo
2) Remover um intervalo
3) Dado um intervalo de x, descobrir se x sobrepõe a qualquer um dos intervalos existentes.

Árvore de Intervalo: A idéia é implementar uma Árvore Binária de busca auto-balanceada (BST) como árvore Preto Vermelho, Árvore AVL, etc Para manter um conjunto de intervalos para que todas as operações possam ser feitas em tempo O(log n).

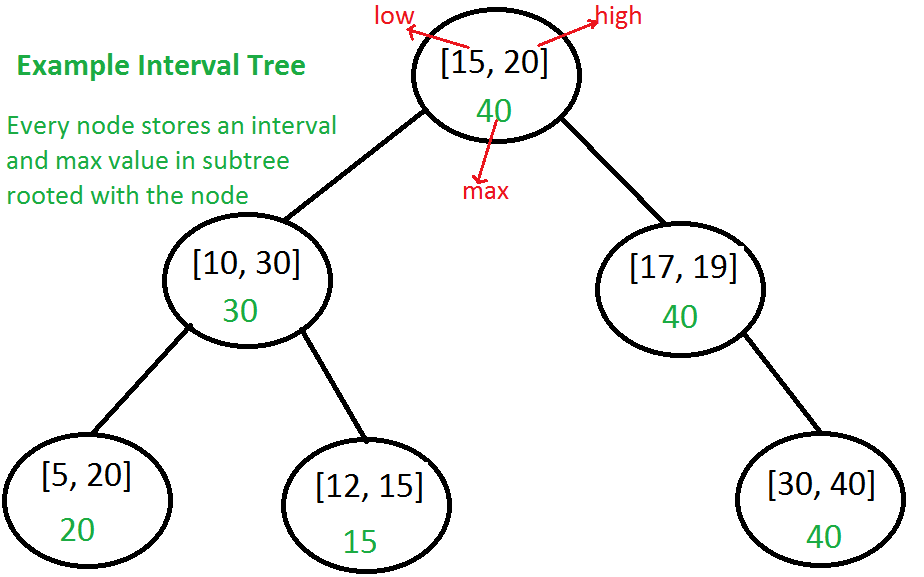
Cada nó da Árvore de Intervalo armazena as seguintes informações.
a) i: Um intervalo que é representado como um par [low, high]
b) máx: valor máximo em subárvore enraizada com este nó.

O valor "low" de um intervalo é usado como chave para manter a ordem no BST. A inserção e exclusão de operações são as mesmas de inserção e exclusão em BST auto-balanceada usada.

A principal operação é a busca de um intervalo de sobreposição. A seguir está o algoritmo para pesquisar um intervalo de sobreposição x em uma árvore enraizada com Interval raiz.

Intervalo overlappingIntervalSearch (raiz, x)
1) Se x sobrepõe com intervalo de raiz, retornar intervalo da raiz.
2) Se o filho da esquerda da raiz não está vazio e o valor máximo no filho da esquerda é maior do que o valor mínimo de x, recorrer para filho esquerdo
3) Senão recorrer para o filho direito.

Como o algoritmo acima funciona?
Sendo x o intervalo a ser procurado. Precisamos provar isso para os seguintes dois casos.

Caso 1: Quando vamos a subárvore direita, um dos seguintes procedimentos devem ser verdadeiras.
a) Existe uma sobreposição na subárvore direita: Isso é bom, precisamos voltar um intervalo de sobreposição.
b) Não existe qualquer sobreposição em qualquer subárvore: Vamos para subárvore direita apenas quando a esquerda é NULL ou valor máximo na esquerda é menor do que x.low. Assim, o intervalo não pode estar presente na sub-árvore para a esquerda.

Caso 2: Quando vamos a subárvore esquerda, um dos seguintes procedimentos deve ser verdadeiro.
a) Existe uma sobreposição na subárvore esquerda: Isso é bom, precisamos voltar um intervalo de sobreposição.
b) Não existe qualquer sobreposição em qualquer subárvore: Esta é a parte mais importante. Precisamos considerar seguintes fatos.
... Fomos a subárvore esquerda, porque x.low está na subárvore esquerda
.... max na subárvore esquerda é o maior de um dos intervalos digamos [a, max] na subárvore esquerda.
.... Como x não se sobrepõe com qualquer nó no x.low da subárvore esquerda deve ser menor que 'a'.
.... Todos os nós no BST são ordenados pelo menor valor, assim todos os nós na subárvore direita deve ter um valor maior que 'a'.
.... A partir dos dois fatos acima, podemos dizer todos os intervalos na subárvore direita têm valor o seu menor valor maior que x.low. Então x não pode se sobrepor a qualquer intervalo na sub-árvore direita.

Implementação da Árvore de intervalo:
A seguir está a implementação da Árvore de intervalo. A aplicação usa uma operação básica de inserção de BST para manter as coisas simples. Idealmente, deve ser inserção de Árvore AVL ou inserção de árvore vermelha e preta.

#include <iostream>
using namespace std;
// Structure to represent an interval
struct Interval
{
    int low, high;
};
// Structure to represent a node in Interval Search Tree
struct ITNode
{
    Interval *i; // 'i' could also be a normal variable
    int max;
    ITNode *left, *right;
};
// A utility function to create a new Interval Search Tree Node
ITNode * newNode(Interval i)
{
    ITNode *temp = new ITNode;
    temp->i = new Interval(i);
    temp->max = i.high;
    temp->left = temp->right = NULL;
};
// A utility function to insert a new Interval Search Tree Node
// This is similar to BST Insert. Here the low value of interval
// is used tomaintain BST property
ITNode *insert(ITNode *root, Interval i)
{
    // Base case: Tree is empty, new node becomes root
    if (root == NULL)
        return newNode(i);
    // Get low value of interval at root
    int l = root->i->low;
    // If root's low value is smaller, then new interval goes to
    // left subtree
    if (i.low < l)
        root->left = insert(root->left, i);
    // Else, new node goes to right subtree.
    else
    root->right = insert(root->right, i);
    // Update the max value of this ancestor if needed
    if (root->max < i.high)
        root->max = i.high;
    return root;
}
// A utility function to check if given two intervals overlap
bool doOVerlap(Interval i1, Interval i2)
{
    if (i1.low <= i2.high && i2.low <= i1.high)
        return true;
    return false;
}
// The main function that searches a given interval i in a given
// Interval Tree.
Interval *overlapSearch(ITNode *root, Interval i)
{
    // Base Case, tree is empty
    if (root == NULL) return NULL;
    // If given interval overlaps with root
    if (doOVerlap(*(root->i), i))
        return root->i;
    // If left child of root is present and max of left child is
    // greater than or equal to given interval, then i may
    // overlap with an interval is left subtree
    if (root->left != NULL && root->left->max >= i.low)
        return overlapSearch(root->left, i);

    // Else interval can only overlap with right subtree
    return overlapSearch(root->right, i);
}
void inorder(ITNode *root)
{
    if (root == NULL) return;
    inorder(root->left);
    cout << "[" << root->i->low << ", " << root->i->high << "]" << " max = " << root->max << endl;
    inorder(root->right);
}
// Driver program to test above functions
int main()
{
    // Let us create interval tree shown in above figure
    Interval ints[] = {{15, 20}, {10, 30}, {17, 19}, {5, 20}, {12, 15}, {30, 40}};
    int n = sizeof(ints)/sizeof(ints[0]);
    ITNode *root = NULL;
    for (int i = 0; i < n; i++)
        root = insert(root, ints[i]);
    cout << "Inorder traversal of constructed Interval Tree is\n";
    inorder(root);
    Interval x = {6, 7};
    cout << "\nSearching for interval [" << x.low << "," << x.high << "]";
    Interval *res = overlapSearch(root, x);
    if (res == NULL)
        cout << "\nNo Overlapping Interval";
    else
        cout << "\nOverlaps with [" << res->low << ", " << res->high << "]";
    return 0;
}

Saída:
Inorder traversal of constructed Interval Tree is
[5, 20] max = 20
[10, 30] max = 30
[12, 15] max = 15
[15, 20] max = 40
[17, 19] max = 40
[30, 40] max = 40
Searching for interval [6,7]
Overlaps with [5, 20]
Aplicações da Árvore de Intervalos:
Árvore de intervalo é principalmente uma estrutura de dados geométrica e, muitas vezes usado para consultas de janelas, por exemplo, para encontrar todas as estradas em um mapa dentro de uma área visível retangular, ou para encontrar todos os elementos visíveis dentro de uma cena tridimensional.

Árvore de Intervalos vs Árvore de Segmentos
Árvores de segmentos e de intervalos armazenam intervalos. Árvore de Segmentos são otimizadas para buscas por um dado ponto, e árvores de intervalo são otimizadas para buscas de sobreposição em um dado intervalo.


Fonte:
http://www.geeksforgeeks.org/interval-tree/

Referências:
http://en.wikipedia.org/wiki/Interval_tree
http://www.cse.unr.edu/~mgunes/cs302/IntervalTrees.pptx
Introduction to Algorithms 3rd Edition by Clifford Stein, Thomas H. Cormen,
Charles E. Leiserson, Ronald L. Rivest
https://www.youtube.com/watch?v=dQF0zyaym8A