Uma árvore de busca ternária é uma estrutura especial de dados Trie onde os nós filhos de um Trie padrão são ordenados como uma árvore de busca binária.

Representação de árvores de busca ternárias:

Ao contrário de estrutura de dados Trie (padrão), onde cada nó contém 26 indicadores para os seus filhos, cada nó em uma árvore de busca ternária contém apenas três ponteiros:
1. O ponteiro da esquerda aponta para o nó cujo valor é menor que o valor no nó atual.
2. O ponteiro central aponta para o nó cujo valor é igual ao valor do nó atual.
3. O ponteiro da direita aponta para o nó cujo valor é maior do que o valor no nó atual.

Além dos três ponteiros acima, cada nó tem um campo para indicar dados (caracteres em caso de dicionário) e um outro campo para marcar extremidade de uma string.
Então, mais ou menos, é semelhante a BST que armazena dados com base em alguma ordem. No entanto, os dados em uma árvore de busca ternária é distribuído sobre os nós. por exemplo. São necessários 4 nós para armazenar a palavra "Geek".
A figura abaixo mostra como exatamente as palavras em uma árvore de busca ternária são armazenados?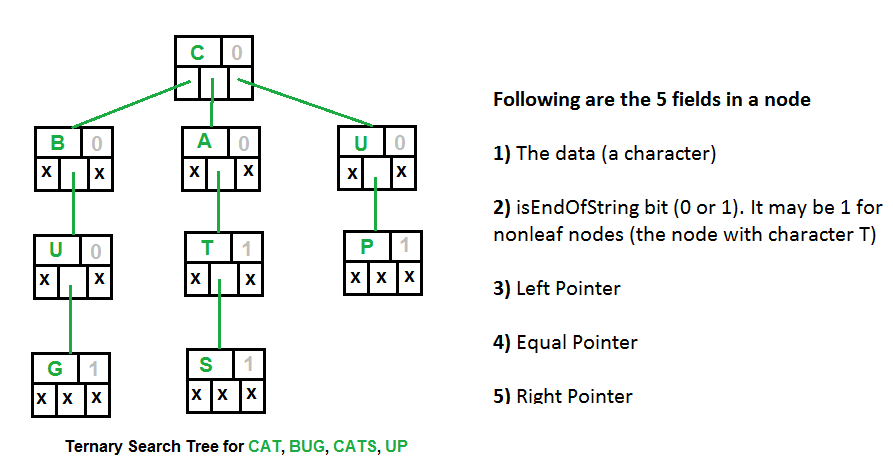



Uma das vantagens do uso de árvores de pesquisa ternárias sobre Tries é que as árvores de pesquisa ternárias usam menos espaço (envolvem apenas três ponteiros por nó em comparação com 26 em Tries convencionais).

Tries são adequados quando existe uma distribuição adequada de palavras sobre os alfabetos para que os espaços sejam utilizados de forma mais eficiente. Caso contrário árvores de busca ternárias são melhores. Árvores de busca ternárias são eficientes para usar (em termos de espaço) quando as strings a serem ser armazenadas compartilham um prefixo comum.

Aplicações de árvores de busca ternárias:

1. árvores de busca ternárias são eficientes para consultas como "Dada uma palavra, encontrar a próxima palavra no dicionário (pesquisas de vizinhos)" ou "Encontre todos os números de telefone que começam com 9342 ou" digitando alguns caracteres iniciais em um navegador da Web exibe todos os site cujo nomes tem esse prefixo "(recurso de auto-complete)".
2. usado em verificador ortográfico: árvores de busca ternárias pode ser utilizada como um dicionário para guardar todas as palavras. Uma vez que a palavra é digitada em um editor, a palavra pode ser paralelamente procurada na árvore de busca ternária para verificar a ortografia correta.

Implementação:
Na sequência está a implementação C da árvore de busca ternária. As operações implementadas são, busca, inserção e transversal.

// C program to demonstrate Ternary Search Tree (TST) insert, travese
// and search operations
#include <stdio.h>
#include <stdlib.h>
#define MAX 50
// A node of ternary search tree
struct Node
{
    char data;
    // True if this character is last character of one of the words
    unsigned isEndOfString: 1;
    struct Node *left, *eq, *right;
};
// A utility function to create a new ternary search tree node
struct Node* newNode(char data)
{
    struct Node* temp = (struct Node*) malloc(sizeof( struct Node ));
    temp->data = data;
    temp->isEndOfString = 0;
    temp->left = temp->eq = temp->right = NULL;
    return temp;
}
// Function to insert a new word in a Ternary Search Tree
void insert(struct Node** root, char *word)
{
    // Base Case: Tree is empty
    if (!(*root))
        *root = newNode(*word);
    // If current character of word is smaller than root's character,
    // then insert this word in left subtree of root
    if ((*word) < (*root)->data)
        insert(&( (*root)->left ), word);
    // If current character of word is greate than root's character,
    // then insert this word in right subtree of root
    else if ((*word) > (*root)->data)
        insert(&( (*root)->right ), word);
    // If current character of word is same as root's character,
    else
    {
        if (*(word+1))
            insert(&( (*root)->eq ), word+1);
        else
            // the last character of the word
            (*root)->isEndOfString = 1;
    }
}
// A recursive function to traverse Ternary Search Tree
void traverseTSTUtil(struct Node* root, char* buffer, int depth)
{
if (root)
{
    // First traverse the left subtree
    traverseTSTUtil(root->left, buffer, depth);
    // Store the character of this node
    buffer[depth] = root->data;
    if (root->isEndOfString)
    {
        buffer[depth+1] = '\0';
        printf( "%s\n", buffer);
    }
    // Traverse the subtree using equal pointer (middle subtree)
    traverseTSTUtil(root->eq, buffer, depth + 1);
    // Finally Traverse the right subtree
    traverseTSTUtil(root->right, buffer, depth);
}
}
// The main function to traverse a Ternary Search Tree.
// It mainly uses traverseTSTUtil()
void traverseTST(struct Node* root)
{
    char buffer[MAX];
    traverseTSTUtil(root, buffer, 0);
}
// Function to search a given word in TST
int searchTST(struct Node *root, char *word)
{
    if (!root)
        return 0;
    if (*word < (root)->data)
        return searchTST(root->left, word);
    else if (*word > (root)->data)
        return searchTST(root->right, word);
    else
    {
        if (*(word+1) == '\0')
            return root->isEndOfString;
        return searchTST(root->eq, word+1);
    }
}
// Driver program to test above functions
int main()
{
    struct Node *root = NULL;
    insert(&root,"cat");
    insert(&root,"cats");
    insert(&root,"up");
    insert(&root,"bug");
    printf("Following is traversal of ternary search tree\n");
    traverseTST(root);
    printf("\nFollowing are search results for cats, bu and cat respectively\n");
    searchTST(root, "cats")? printf("Found\n"): printf("Not Found\n");
    searchTST(root, "bu")? printf("Found\n"): printf("Not Found\n");
    searchTST(root, "cat")? printf("Found\n"): printf("Not Found\n");
    return 0;
}

Saída:
Following is traversal of ternary search tree
bug
cat
cats
up
Following are search results for cats, bu and cat respectively
Found
Not Found
Found

Complexidade de tempo: A complexidade de tempo das operações de uma árvore de busca ternária é similar ao de uma árvore de busca binária, as operações de inserção, remoção e busca tem um tempo proporcional à altura da árvore. O espaço é proporcional ao tamanho da string a ser armazenada.

Referência:
http://en.wikipedia.org/wiki/Ternary_search_tree

Fonte:
http://www.geeksforgeeks.org/ternary-search-tree/