
Descrição
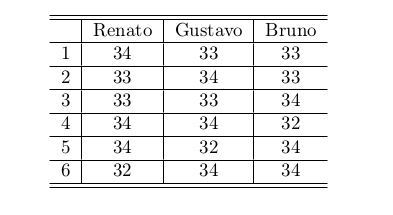
A caixinha contém N palitos de picolé, que precisam ser divididos entre os amigos Renato, Gustavo e Bruno, para um trabalho escolar. Cada amigo deve ganhar pelo menos 1 (um) palito. O professor vai determinar um número M máximo de palitos que cada um pode ganhar. Nesta tarefa, dados N e M , seu programa deve calcular quantas maneiras distintas existem de se dividir todos os N palitos entre os três amigos. Por exemplo, para N = 100: se M = 15, então há zero maneiras de se dividir, pois a soma dos números de palitos de Renato, Gustavo e Bruno seria no máximo 45, só que precisa ser sempre N ; mas se M = 34, aí veja que haveria 6 maneiras distintas:
Entrada
A entrada é composta por apenas uma linha com dois números naturais N e M , indicando, respectivamente, o número de palitos na caixinha e o número máximo que cada amigo pode ganhar.
Saída
Seu programa deve escrever uma única linha na saída, contendo um único número natural: quantas
maneiras distintas existem de se dividir os N palitos entre os três amigos.
Restrições
• 3 ≤ N ≤ 100000, 1 ≤ M ≤ N ;
| Exemplos de Entrada | Exemplos de Saída |
|---|---|
|
100000 98765 |
4997567718 |
|
100 15 |
0 |
|
100 34 |
6 |
Efetue Login ou Cadastre-se para submeter uma solução.
Adaptado por Erich Rodrigues | Competição: OBI 2015, Nível 2, Fase 1