
Descrição
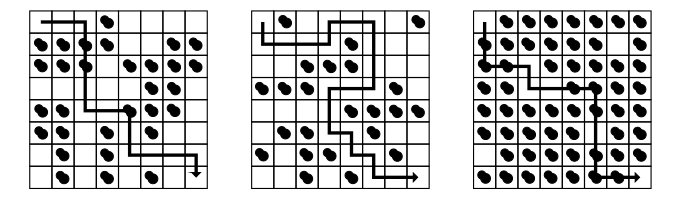
Nossa mina de ouro será representada por N linhas e N colunas de quadrados. O mineiro está no quadrado inicial (superior esquerdo) e precisa cavar até o quadrado final (inferior direito), onde existe a maior concentração de ouro da mina. Alguns quadrados, porém, estão bloqueados por pedras, o que dificulta o trabalho. Sabendo que o mineiro pode realizar apenas movimentos ortogonais, seu programa deve calcular o número mínimo de quadrados bloqueados pelos quais o mineiro tem que passar para chegar no quadrado inferior direito. Os quadrados inicial e final nunca estão bloqueados. A figura abaixo ilustra três possíveis minas, para N = 8, para as quais os números mínimos de quadrados bloqueados são, respectivamente, três, zero e nove. A figura também mostra três possíveis trajetórias mínimas, como exemplo.
Entrada
A primeira linha da entrada contém um inteiro N , 2 ≤ N ≤ 100, representando as dimensões da mina. Cada uma das N linhas seguintes contém N inteiros, definindo os quadrados da mina. O inteiro 0 representa um quadrado livre e o inteiro 1, um quadrado bloqueado.
Saída
Seu programa deve produzir uma única linha, contendo um único inteiro, o número mínimo de quadrados bloqueados pelos quais o mineiro tem que passar para chegar no quadrado final.
| Exemplos de Entrada | Exemplos de Saída |
|---|---|
|
2 |
0 |
|
6 |
3 |
Efetue Login ou Cadastre-se para submeter uma solução.
Adaptado por Erich Rodrigues | Competição: OBI 2015, Nível 2, Fase 2