
Descrição
Em uma floresta há N árvores alinhadas. A i-ésima árvore tem altura Hi e está localizada na posição Xi da floresta. Obi, o macaco camarada, está na primeira árvore da floresta, e deseja ir até a última árvore da floresta, porque ele ouviu dizer que há muitas bananas esperando por ele lá.
Para ir até a última árvore, Obi vai pular entre as árvores. Obi é um macaco muito ágil, e consegue pular de uma árvore A para outra árvore B sempre que, do topo da árvore A ele consegue enxergar o topo da árvore B, independente das posições das árvores A e B. Mas Obi é também um macaco muito preguiçoso, e quer pular o menor número de vezes possível.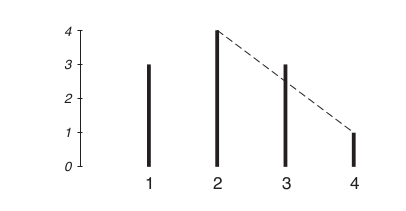
Na figura acima podemos ver que, do topo da árvore na posicão 2, Obi não consegue enxergar o topo da árvore na posição 4, e portanto ele não pode pular de uma para outra sem passar pela árvore na posição 3. Assim, para o caso da figura acima, para ir da árvore 1 para a árvore 4 ele tem que passar por todas as árvores, dando um total de três pulos.
Dada a descrição da floresta, você deve escrever um programa para determinar o menor número de pulos que Obi deve dar para ir da primeira à última árvore da floresta.
Entrada
A primeira linha da entrada contém um número N , indicando a quantidade de árvores na floresta. Cada uma das N linhas seguintes descreve uma árvore da floresta, e contém dois inteiros Xi e Hi, respectivamente a posição e a altura de uma árvore. Cada árvore ocupa uma posição distinta na floresta (ou seja, não há duas árvores com o mesmo valor Xi ).
Saída
Seu programa deve produzir uma única linha, contendo um único número inteiro, a menor a quantidade de pulos que Obi deve dar para ir da primeira até a última árvore da floresta.
Restrições
• 2 ≤ N ≤ 3 × 10^5
• 1 ≤ Hi , Xi ≤ 10^9
| Exemplos de Entrada | Exemplos de Saída |
|---|---|
|
10 |
3 |
|
4 |
2 |
|
4 |
3 |
Efetue Login ou Cadastre-se para submeter uma solução.
Adaptado por Erich Rodrigues | Competição: OBI 2015, Nível 2, Fase 2