
Descrição
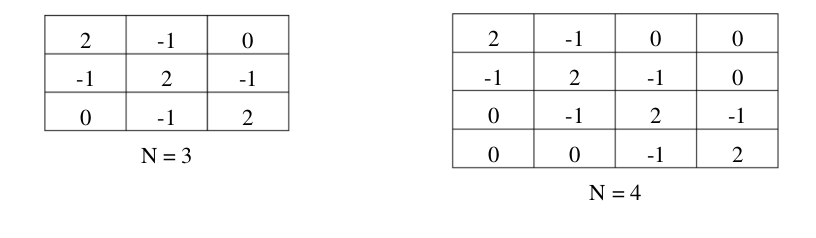
Neste problema você colocará à prova todo o seu grande conhecimento sobre álgebra linear, acumulado por todo o ensino médio, cursinho e faculdade. Estamos interessados em um tipo muito especial de matriz quadrada: todos os elementos de sua diagonal principal possuem o valor 2; as diagonais secundárias imediatamente acima e abaixo da diagonal principal possuem o valor -1; os elementos restantes da matriz possuem o valor zero. As figuras abaixo mostram exemplos desse tipo de matriz. Vamos chamar de "esparsa" uma matriz que possua um valor zero na maior parte de seus elementos. Sua tarefa é, para um dado tamanho de matriz do tipo descrito anteriormente, determinar se a mesma é esparsa ou não.
Entrada
Inicialmente um valor Q é informado, indicando a quantidade de casos de teste a serem processados. Seguem-se Q linhas, cada uma contendo um inteiro N indicando a quantidade de linhas da matriz a ser considerada. O valor de Q será um inteiro positivo menor ou igual a 100, e o valor de N será um inteiro positivo maior ou igual a 2 e menor ou igual a 100000.
Saída
Para cada caso de teste, imprima a letra S (em maiúscula) se a matriz for esparsa ou N (também em maiúscula) caso a matriz não o seja. Em ambos os casos, imprimir após a letra um inteiro indicando a quantidade de elementos com zero na matriz.
| Exemplos de Entrada | Exemplos de Saída |
|---|---|
|
5 |
N 6 |
Efetue Login ou Cadastre-se para submeter uma solução.
Criado por Antonio Cesar de Barros Munari (Fatec Sorocaba) | Adaptado por Erich Rodrigues | Competição: Interfatecs 2015