uCoder | 1079 | Nível: 3 | Tempo Limite: 10
Calendário Maia
Adaptado por Erich Rodrigues
Competição: Interfatecs 2015
Usando seus conhecimentos de astronomia e matemática, os Maias desenvolveram um dos sistemas de calendário mais precisos da história da humanidade. Este sistema de calendários se baseia em diferentes ciclos de variados tamanhos. Os três mais conhecidos são: o calendário Haab, o qual considera os 365 dias do calendário solar e é usado como calendário civil; o Tzolk‟in, é o calendário sagrado com ciclos de 260 dias baseado nos nove ciclos da Lua e no período de gestação humana; e o calendário de Contagem Longa, usado para registrar eventos míticos e históricos.
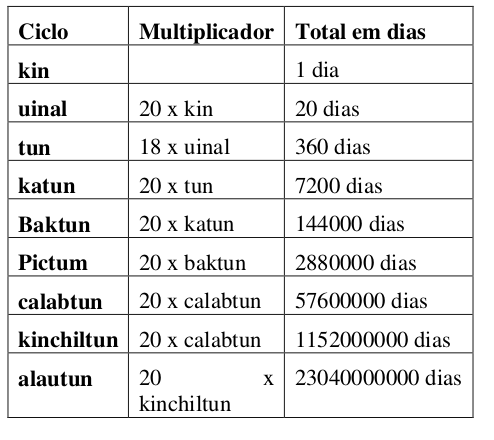
O Calendário de Contagem Longa é um sistema composto por uma hierarquia de ciclos de tempo, similar ao calendário Gregoriano que conta dias, meses, anos, séculos e milênios. Entretanto, como na matemática Maia, o calendário de Contagem Longa utiliza a base 20 na contagem dos ciclos, com exceção do terceiro ciclo, o qual utiliza 18x20, resultando em um ciclo de 360 dias, que é mais próximo do ciclo solar de 365 dias. A tabela 1 mostra estes ciclos.
Utilizando este sistema de contagem vigesimal modificado, este calendário conta os dias decorridos desde a data zero correspondente a 11 de agosto de 3113 a.C. (antes de Cristo) no calendário gregoriano. Embora seja composto por 9 ciclos, os achados arqueológicos mostram que os maias só utilizavam os 5 primeiros ciclos para registrar datas do passado, presente e futuro. Por exemplo, a data 20/10/1991 é escrita em Contagem Longa como sendo:
Ou seja, passaram-se 1.864.267 dias após a data zero (11/08/3113 a.C.).
Sua tarefa neste problema será construir uma calculadora para converter uma data no formato Gregoriano (dia/mês/ano) para o formato do calendário maia.
Entrada
Cada linha da entrada é composta por uma data no formato D/M/A, onde D, M, A são números inteiros e correspondem a uma data gregoriana. Note que as datas anteriores ao nascimento de Cristo estarão representadas pelo valor negativo do Ano (A). Lembre-se que um ano Gregoriano tem 365 dias, ou 366 em casos de anos bissextos onde o mês de fevereiro tem 29 dias. O ano é bissexto quando é divisível por 4, exceto para anos divisíveis por 100 que, para serem bissextos, devem ser divisíveis também por 400. Assim, o ano 2000 é bissexto (divisível por 4, 100 e 400), mas os anos 1700, 1800 e 1900 NÃO são bissextos. Considere que 1 ≤ D ≤ 31; 1 ≤ M ≤ 12, -3113 ≤ A ≤ 4000. Considere também que todas as datas serão iguais ou posteriores a 11/8/3113 a.C.
Saída
Para cada data gregoriana da entrada, imprima na saída a data equivalente no formato Contagem Longa do calendário maia, considerando somente os 5 ciclos na forma: baktun.katun.tun.uinal.kin
| Exemplo de Entrada | Exemplo de Saída |
|---|---|
|
11/8/-3113 |
0.0.0.0.0 |