Descrição
Existem diversas formas práticas de compactação de informação, que fazem o seu trabalho por meio da eliminação de redundâncias presentes no contexto que se está analisando. Uma forma bastante interessante é por meio de estruturas denominadas Quadtree, que permitem uma decomposição recursiva do espaço. Uma quadtree é uma árvore onde todos os nós são folhas ou então possuem grau igual a 4. No caso mais simples, podemos assumir que as regiões de um espaço podem conter dois tipos de informação, que representaremos por zeros e uns neste problema. A ideia básica é subdividir o espaço em 4 partes, e atribuir a cada parte um valor 0 se aquela parte contiver apenas zeros, 1 se contiver apenas uns ou então 2, se a parte tiver tanto zeros como uns. Partes do tipo 2 são então subdivididas em 4 partes menores, e o processo continua até que não tenhamos quaisquer partes do tipo 2.
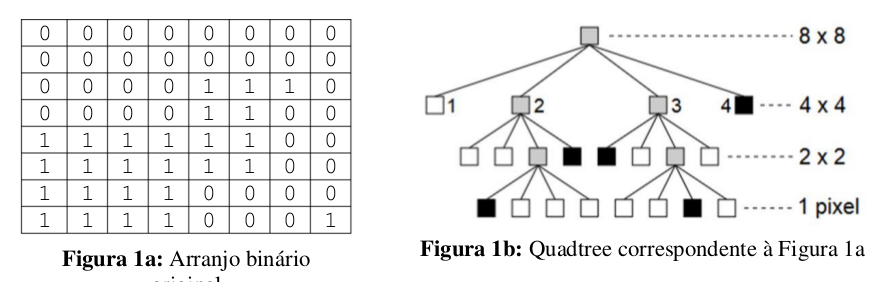Na Figura 1 temos um arranjo binário disposto em um formato 8x8. A Figura 1a mostra o arranjo espacial na matriz quadrada subjacente, a Figura 1b mostra a quadtree correspondente. Na árvore a raiz corresponde à matriz 8x8, que contém tanto zeros como uns. Isso faz com que a raiz tenha valor 2 (indicado pela cor cinza na figura). Subdividimos então essa área não homogênea 8x8 em 4 pedaços 4x4: um no quadrante superior esquerdo, outro no superior direito, outro no quadrante inferior direito e outro no quadrante inferior esquerdo. O primeiro desses quadrantes tem apenas valores zero, então seu valor é zero (indicado pela cor branca do nó marcado com „1‟ na quadtree. O quadrante inferior esquerdo, por sua vez, possui apenas células (ou pixels) com valor um, então o quadrante inteiro tem valor 1 (indicado pela cor preta do nó marcado com „4‟ na quadtree). Os quadrantes restantes possuem tanto zeros como uns e estão marcados com cinza na figura, indicando que não são homogêneos e, por esse motivo, precisam ser subdivididos em arranjos 2x2. A quadtree da Figura 1b pode também ser expressa de forma textual como mostrado a seguir, onde o primeiro inteiro da primeira linha indica a quantidade de linhas do arranjo NxN e o segundo valor indica a cor do nó raiz da quadtree, seguindo-se então uma linha para cada nível da árvore, no sentido da esquerda para a direita:
8 2
0221
0021
1020
1000
0010
Sua tarefa neste problema será gerar a representação textual da quadtree correspondente a um arranjo binário NxN lido da entrada.
Entrada
Cada caso de teste é iniciado por um inteiro N, 4 ≤ N ≤ 512, em que N é uma potência de 4 e indica a medida de cada lado do arranjo binário NxN a ser processado. Seguem-se então N linhas, cada uma contendo N valores V separados por um espaço em branco, onde o valor de V será sempre igual a zero ou a um. A entrada é finalizada com um valor N = 0, que não deverá ser processado.
Saída
Para cada caso de teste, imprima a representação textual da quadtree, conforme explicado anteriormente e ilustrado nos exemplos.
| Exemplos de Entrada | Exemplos de Saída |
|---|---|
|
8 |
8 2 |
Efetue Login ou Cadastre-se para submeter uma solução.
Criado por Antonio Cesar de Barros Munari (Fatec Sorocaba) | Adaptado por Erich Rodrigues | Competição: Interfatecs 2015