
Descrição
A sala de aulas utilizada para os cursos da OBI tem uma grande janela, composta de três folhas de vidro. A janela tem um metro de altura por seis metros de comprimento. Cada folha da janela tem um metro de altura e dois metros de comprimento. As folhas deslizam sobre trilhos, ao longo do comprimento da janela, de forma que é possível controlar a abertura da janela, para circulação de ar.
Dadas as posições das três folhas da janela, deseja-se determinar qual a área da janela que está aberta, em centímetros quadrados.
A figura abaixo ilustra duas configurações das folhas da janela. Na figura, os cantos inferiores esquerdos de cada folha são indicados por F1,F2 e F3. Na configuração (a) a janela está totalmente fechada, e portanto o total da área aberta é igual a zero. Na configuração (b) há duas aberturas, e o total de área aberta é igual a (100 × 100) + (50 × 100) = 15.000 cm².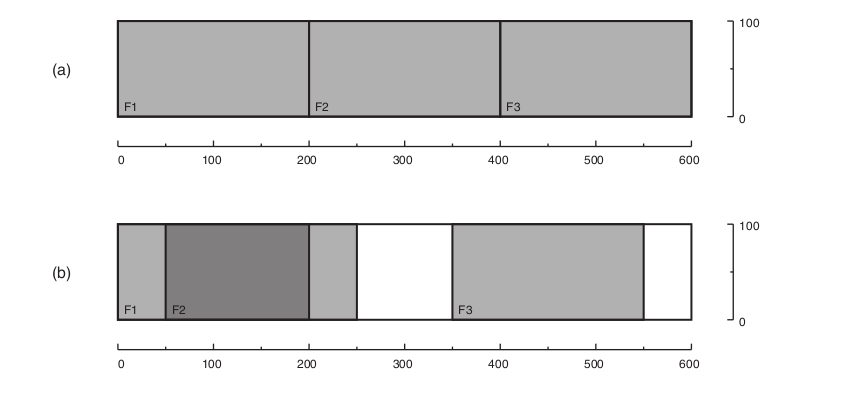
Dadas as posições das três folhas da janela, escreva um programa que calcule a área da janela que está aberta, em centímetros quadrados.
Entrada
A primeira e única linha da entrada contém três inteiros F1 , F2 e F3 , indicando as posições das três folhas. A posição de cada folha é dada pela distância, em centímetros, da extremidade esquerda da janela até a extremidade esquerda da folha.
Saída
Seu programa deve imprimir uma única linha, contendo um único inteiro, a área aberta da janela em centímetros quadrados.
Restrições
• 0 ≤ F1 , F2 , F3 ≤ 400.
| Exemplos de Entrada | Exemplos de Saída |
|---|---|
|
344 344 344 |
40000 |
|
0 50 350 |
15000 |
|
0 200 400 |
0 |
Efetue Login ou Cadastre-se para submeter uma solução.
Adaptado por Erich Rodrigues | Competição: OBI 2013, Nível 2, Fase 2