
Descrição
Um quadrado quase mágico, de dimensões N × N , é um quadrado que obedece à seguinte condição. Existe um número inteiro positivo M tal que: para qualquer linha, a soma dos números da linha é igual a M ; e para qualquer coluna, a soma dos números da coluna é também igual a M . O quadrado seria mágico, e não apenas quase mágico, se a soma das diagonais também fosse M . Por exemplo, a figura abaixo, parte (a), apresenta um quadrado quase mágico onde M = 21.
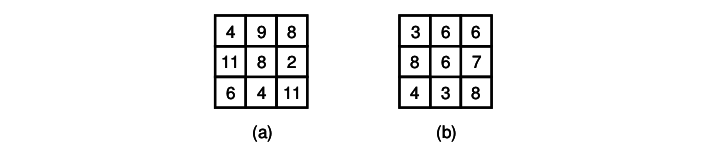
Laura construiu um quadrado quase mágico e alterou, propositalmente, um dos números! Nesta tarefa, você deve escrever um programa que, dado o quadrado quase mágico alterado por Laura, descubra qual era o número original antes da alteração e qual número foi colocado no lugar. Por exemplo, na parte (b) da figura, o número original era 1, que Laura alterou para 7.
Entrada
A primeira linha da entrada contém apenas um número N , representando a dimensão do quadrado. As N linhas seguintes contêm, cada uma, N números inteiros, definindo o quadrado. A entrada é garantidamente um quadrado quase mágico onde exatamente um número foi alterado.
Saída
Seu programa deve imprimir apenas uma linha contendo dois números: primeiro o número original e depois o número que Laura colocou no seu lugar.
Restrições
• 3 ≤ N ≤ 50; e o valor de todos os números está entre 1 e 10000
| Exemplos de Entrada | Exemplos de Saída |
|---|---|
|
3 |
1 7 |
Efetue Login ou Cadastre-se para submeter uma solução.
Adaptado por erich.rodriguesf | Competição: OBI 2014, Nível 1, Fase 2